Description of Model

Channel Flow Modelling

A Simple Von-Karman Turbulant Boundary Layer Calculation Scheme:

Utilising the Coles velocity profile, above, and a skin friction correlation formula, the velocity profile may be calculated, with specified skin friction and bulk characteristics. We need the equations here. The calculation proceeds as follows:

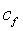1. assumed and external velocity distribution defined
2. H calculated by inverting expression for 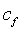(eqn 2)
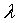3. from (eqn 3)
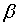4. from (5)
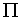5. from (4)
6. H from (6 & 7)
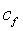7. from H & repeat until convergence

back to top

Effects of Roughness

As described elsewhere, the Manning’s roughness coefficient is used in classical open channel hydrodynamics to relate flow velocity to bed roughness. It is this relation that will allow us to develop a relation between wall shearing stress and seabed medium as follows. (6)

The Manning equation:

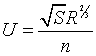
Where n is the Manning’s number of the channel, S is the slope in terms of rise upon run, and R is the hydraulic radius. The Manning number may be related to the size of the gravel or sand or rocks on the seabed by the Strickler relationship:

For D in metres. This allows us to say, for example, that large rocks with a 0.5m diameter have a Manning’s number of about 0.0356 and so on, and the upshot is that larger seabed media is rougher in terms of velocity (and thus skin friction).
If the Manning’s equation is multiplied by and rearranged

Then raised to the power 1.5 we have with n as the overall channel Manning’s number, accounting for meander, bed roughness, constriction and so on. Thus the contribution to the wall shearing stress due to bottom roughness alone may be written as

And this is the value used to calculate the skin friction due to bottom roughness in the above boundary layer calculation, since:

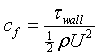
We now have all the parameters required to plot a Cole’s law profile (eqn 1) for our turbulent BL.

back to top

 

 

Description of Model

Channel Flow Modelling

Go back to Contents