| Thermal storage consists in storing heat in a medium for later use. The storage of heat over short term period (a few hours or days) can be achieved relatively easily using standard high thermal mass materials such as water, concrete or brick. For instance, standard insulated hot water tanks working on cheaper night time electricity rate will keep the water fairly warm for at least 2 days. Another example is the use of thermal mass materials in the floor or walls of a house will allow storing heat effectively over a daily cycle (see the ESP-r modeling summary and the ESP-r analytical). This form of storage would not be adequate when there is a large temporal mismatch between surplus heat generation and subsequent requirement. In this case we must consider seasonal storage which is about longer term heat storage, typically over periods of weeks or month, which is a bigger challenge. Solar water heating systems are now standard equipment available about everywhere and in some countries (Israel) they have become the standard water heating system. One problem is they tend to generate a lot of excess heat during summer months in particular, and in a large proportion of European climate the surplus heat can exceed the actual heat utilised immediately. Without some form of long term storage the heat is always lost. It makes sense to evaluate the potential of a hybrid system that would allow in some way to maximise the efficiency of the solar heating system by storing (some of) the excess heat produced in summer. Seasonal heat storage however is only useful if the solar heating system (or other renewable source in place) generates a reasonable proportion of the heating demand required in the winter. This form of hybrid system between a solar heat source and a large long term storage capacity resource would offer obvious benefits.
Approach
Apart from the cost of the systems itself, which depends largely on the type of storage and the specific situation, there are a number of critical parameters to be analysed when considering seasonal storage.
- Capacity requirement:
The difficulty and cost of heat storage is primarily driven by the heat capacity required. It should be essential here not to oversize a system unless there is a clear benefit to it. The size of the system for a given capacity will depend upon the type of storage and the conditions of storage. For instance higher sensible heat storage temperature will allow reducing the size of the system but heat losses will increase. While it is true that a large installation has more constraints on space, infrastructure and cost it is also true that large systems in general can be more effective on a pro-rata basis.
- Output temperature / storage temperature:
For a given size system and storage temperature (sensible heat storage) the system capacity will depend on the output (retrieval) temperature. The lower it is, the higher the heat capacity of the system is because the temperature difference is higher. Similarly, for a given output temperature, capacity will increase with the storage temperature. Note that higher storage temperature will always reduce the efficiency of the system that stores the heat, whether it is solar or heat pump, etc. For a phase change material the output temperature must be below the melting point of the material, the lower it is the better, as we then benefit from additional sensible heat storage capacity.
- Heat losses:
Heat has to be stored at a higher temperature than it will be used so regardless of how well it is insulated there will be some heat losses. The problem is that in seasonal storage heat losses will be higher due to the potentially long period of storage. It seems rather obvious that seasonal storage medium should require good insulation in order to be effective.
- Storage time:
The delay between the time when heat is stored and the time when it is released will also have an impact on the system efficiency. Actually, the longer the time is, the higher the heat losses are. In most of the cases this time delay is difficult to be evaluated. In a typical solar collector heat storage scheme the most important storage period will be mid summer and the time when most heat is required will be about 6 months later, but heat storage will continue beyond the summer and heat retrieval will start probably before the start of the winter.
We will also look at different options of storage. The cases which are considered are:
♦ Water tank
♦ Concrete of rock
♦ PCM (phase change materials)
Results - see the results excel sheet
♦ Water tank (located in basement and well insulated):
Water is a cheap storage medium with high heat capacity = 4.18 kJ/kg/K. Therefore, one cubic meter of water has a heat capacity = 1.16 kWh/K.
Space constraints will limit the storage physical capacity to 50m3 which we consider as a rather decent size for a small individual dwelling with floor space of about 122m2.
- We first model the requirements for storing 1000kWh of heat using hot water
We obtain the graph below based on the following parameters:
◊ Water heat capacity 4.18 kJ/kg/K
◊ Output temperature for use at 28°C (which we considered as a low value for most practical cases, for instance under-floor space heating)
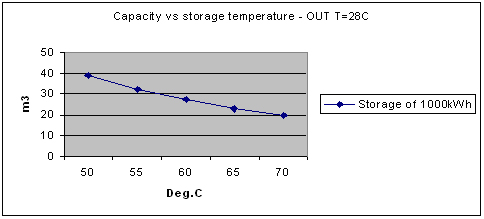
From the above graph we notice that at 70°C about 20m3 of water are required while if the storage temperature is lower; at 50°C then 39m3 are required. Using a storage temperature of 50°C, a storage capacity of 50m3 would therefore allow us to store about 1250kWh (minus losses).
Evaluation of heat losses
There are 2 interesting metrics we can look at on a time basis:
· The storage temperature drop with time
· The remaining heat stored as temperature drops
- We now model how the temperature would change on a daily basis
In order to evaluate how the temperature changes on a daily basis we have made the following assumptions:
◊ No further heat storage and no retrieval of heat
◊ Good insulation around the tank(s) situated in basement: overall U-value (insulation and surrounding building structure is taken at about 0.15 W/m2.K
◊ Ground temperature is 15°C on average during storage period<
◊ Initial storage temperature (at the end of storage period) is 50°C
◊ Output temperature is 28°C
◊ We use 2 tanks: diameter=2.5m x 5.1m length (total 50m3)
We see on the graph below the temperature profile for a period of 100 days.
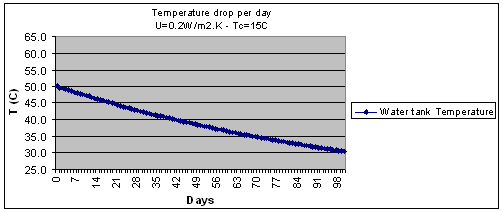
Temperature drop rate is logically higher when the temperature is higher, on average the rate of temperature drop is roughly 0.2°C per day.
We see that the temperature has dropped to below 30°C after 100 days. In other words the heat stored initially has almost entirely been lost.
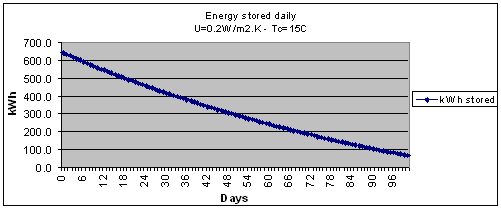
At day 100, there is in each tank 67 kWh left (134 kWh total) from the 639 kWh initially. We can conclude from this result that seasonal storage would not be viable at all in these conditions. In reality a number of things will actually be different as we will not have a 100 days waiting period, and heat may continue to be stored until retrieval of heat starts as well or even during most of the winter. It is also possible that more heat be stored in summer, taking the temperature above 50°C.
Remark
We ran also simulations using one large rectangular tank which benefits from a smaller surface area for the same volume and we obtain a final temperature of 32°C and residual heat load of 200kWh, which is slightly better. The cost of such a tank, compared with standard water storage cylinders would probably not be advantageous. We should now look at the yearly solar heating figures, basically for seasonal storage to be considered we require in the first instance to have an excess of solar heat that sufficiently important in order to justify the installation.
- Solar heat recovered from collectors
We modelled solar heat recovered from collectors located on the roof in both Glasgow and Palermo. We have assumed collector area of 2.8m2 and an efficiency of 60%.
◊ The yearly hot water demand in Glasgow is 3560 kWh and the solar fraction is 47%. ◊ The yearly hot water demand in Palermo is 3051 kWh and the solar fraction is 87%.
In other words looking at the annual energy yield there is no excess apparently available for storage. We know however that these figures do not mean much in terms of excess, in fact solar power is not constant and there will be long period of intensive sun light which will generate an excess, in summer in particular. The graph below shows the solar fraction for hot water heating on a monthly basis.
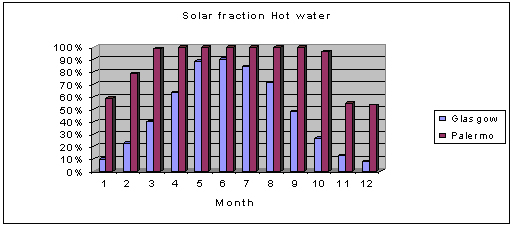
In Glasgow we notice that the solar fraction never reaches 100% while in Palermo it is above 100% from April to September. Therefore, there will be excess heat in Palermo, whereas in Glasgow the resulting solar heat excess is still zero. We therefore have to go further one more step to daily simulation. This now means we compare the amount of heat collected with the demand on a daily basis. This provides a more accurate calculation of the solar heat excess because we now differentiate between sunny days and overcast days within the same month. The following graph shows the solar heat yearly excess for Glasgow and Palermo calculated both on a monthly and daily basis.
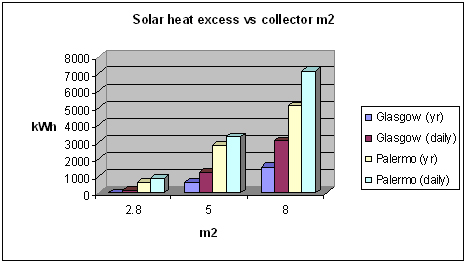
The 2 results obtained for Glasgow are very different; this can be justified by the fact that in a climate such as Glasgow we all know that in summer there can be big differences in solar energy from one day to the next.
◊ For collectors of 2.8m2
- The excess for Glasgow is zero based on monthly calculation, and 161 kWh based on daily calculation.
- In Palermo the excess heat is 871 kWh based upon daily calculation, which seems also small to justify storage requirement but could be considered.
Because our system uses a storage tank which is insulated and can keep water warm for over a day, there is no need to go to more precise calculations. The solar heat collected is used to heat the domestic hot water as it comes available anytime during the day and the excess heat calculated daily represents anything beyond that.
◊ For collectors of 5m2
- Glasgow --> 1219 kWh
- Palermo --> 3333 kWh
◊ For collectors of 8m2
The excess heat becomes quite significant for both Glasgow and Palermo:
- Glasgow --> about 5000 kWh
- Palermo --> about 7000 kWh
We conclude for the moment that:
- In Glasgow, the excess heat generated by solar collectors would potentially justify seasonal storage if the collectors area is more than 5m2, in such case the heat represents more than the space heating demand in our dwelling modelled
- In Palermo the excess heat could become significant enough with collectors of area about 3m2 or more.
- In Palermo, for collectors of 5m2 the excess heat becomes significant for a low consumption individual dwelling.
Palermo:
As we discussed earlier, in order to justify seasonal storage, it is also necessary to have a use some time later for the heat stored. In this particular case our modelling work in Palermo using ESP-r has led us to a space heating demand of nearly zero.There would be no benefits of storing heat in this case for winter use, unless it was for the domestic hot water demand. Hot water however requires to be heated higher than that of low temperature heating systems (such as under-floor); in this case we would need to make use of a heat pump to provide the hot water using the heat from the storage capacity. This solution may be considered whenever suitable, in our case the solar collectors of 2.8m2 do no provide a large amount of excess heat and in addition the deficit solar heat is small and therefore additional investment in a heat pump would normally not be justified.One important point here is in case there was a significant cooling load in summer, then a small reversible ASHP could be used to provide both the summer cooling load and the deficit heat required for domestic hot water.
Glasgow: Seasonal storage tank using 6 m2 of collectors
We will now look at the storage and usage of heat in the hybrid system; we combine results from previous analysis of the tank losses and the surplus heat storage.
We consider a monthly analysis first.
The excess heat from the solar collectors is represented below in blue colour.
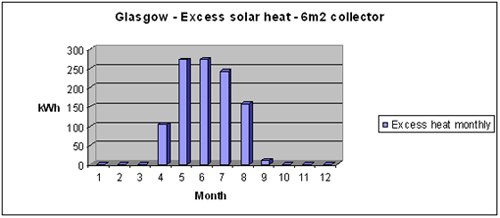
The results on storage tank temperature and heat losses have shown us earlier that after about 100 days of storage any heat load would almost entirely be lost to the external environment. The data tells us also that in the first 30 days we lose about 35% (of original heat load), and about 25% in the next 2 periods of 30 days. The ESP-r data obtained in modelling for a dwelling shows that the space heating monthly for our dwelling of 122m2 is as follows: ◊ October --> 0
◊ November --> 139 kWh
◊ December --> 330 kWh
◊ January --> 380 kWh
◊ February --> 144 kWh
As heating starts in November, it is obvious therefore that all the heat stored in April, May, June, July will be lost before it is needed. The heat stored in August will have reduced to a very small fraction as well. Thus, we can conclude that the seasonal storage option is not a viable option for a dwelling of this type in Glasgow. The main issue is the time lapse between heat storage periods and subsequent heat requirement. Looking at the results above, it is obvious that seasonal storage to be viable would need a much more prolonged heat storage period and also to start using the heat much earlier. Given that after 30 days the heat load is down by 35%, it could be a reasonable statement to say that a kWh stored at any point in time must be used within about a month to make it worthwhile. In this case it seems difficult to envisage that just a standard solar heat excess and heating demand would provide the right opportunity in any part of the year. What is needed is a scheme where the storing of heat comes from various sources, is not concentrated in summer period and at the same time a heat demand from the storage that is more spread in time. This may be achieved on a community scale by combining a number of different input and output options, rather than individual dwelling.
♦ Concrete slab / rock formation:
Given the results obtained for a well insulated water tank, we see few reasons to investigate this scheme. Concrete heat capacity is not as high (~ 1 kJ/kg.K) as water and the problem of insulation and heat losses is essentially the same as for a water tank. It is unlikely from a financial point of view that such an installation, or the drilling of a rock bed would be much cheaper either. Just to mention data and compare with our result we looked at several reports in literature regarding large scale installations of this kind. For instance a system built for seasonal storage in a rock formation in Northern Europe uses:
◊ Solar collectors with fraction equal to 60%
◊ Bore drilling at 65m dept
◊ Storage water temperature 30 to 45C
◊ Storage volume of about 60m3 for each 1000 kWh demand
◊ A final water temperature for space heating of 30C
These are fairly similar parameters to our previous case. The results they obtained was that 42% of solar energy stored was lost, which seems a rather decent result as a matter of fact.
♦ PCM (phase change materials)
Seasonal storage can technically be achieved using phase change materials.
The main problems are the costs of these materials as well as some properties regarding stability. None of these technologies are currently technically mature.
The other thing is that in our specific cases here we would still have to deal with the same heat losses problem and the long period between heat storing and retrieval, which prevents any efficient storing of the heat. What we will therefore limit ourselves to do here is to evaluate the difference between phase change materials (PCM) and water in terms of how much storage capacity they could actually provide, assuming there would be viable commercial options available and the heat storage losses could be made reasonably small. One example of typical inorganic material is Sodium sulphate decahydrate, which melts at 32.4 C and has a latent heat of 252 kJ/kg. The heat capacity (liquid) is about 2.1 kJ/kg.K and the density is about 1.7kg/dm3. We have evaluated the volume required by both the PCM and water to store 1000 kWh of heat. As the PCM melting point is 32.4°C, we take the output temperature for the heat to be 30°C.We also assume both storage medium will be heated to 50°C storage temperature to assess the sensible heat load. The obtained results are:
◊ Using water we require a volume of 43.1m3
◊ Using the PCM we require a volume of just above 7m3
This is a fairly important difference in volume, meaning that a volume of 60m3 could store over 8500 kWh when water could manage only 1250 kWh. This looks rather good. The high latent heat value is what provides the extra storage capacity, despite a sensible heat load half as high for the PCM. The smaller the temperature difference the more advantageous the PCM becomes compared with water.
It is important to note that this PCM material has excellent properties compared with many others.
Conclusions
- Seasonal storage using water or alternative materials is not viable for our case-studies
- The problem of heat losses when storage is too long is an issue for any material
- The main problem in Glasgow is the time lag between heat storage and release and resulting heat losses
- In Palermo there is not a sufficient winter heat requirement to seasonal storage
- Some phase change materials can provide a much better storage capacity than water
http://www.engineeringtoolbox.com/specific-heat-fluids-d_151.htmlhttp://people.bath.ac.uk/absmaw/BEnv1/properties.pdf
| 