Fuzzy controllers are the most important applications of fuzzy theory. They work rather different than conventional controllers; expert knowledge is used instead of differential equations to describe a system. This knowledge can be expressed in a very natural way using linguistic variables, which are described by fuzzy sets.
The problem is to balance a pole on a mobile platform that can move in only
two directions, to the left or to the right.
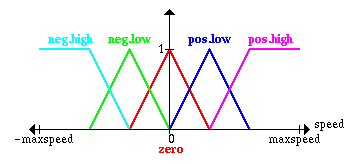
First of all, we have to define (subjectively) what high speed,
low speed etc. of the platform is; this is done by specifying the
membership functions for the fuzzy_sets
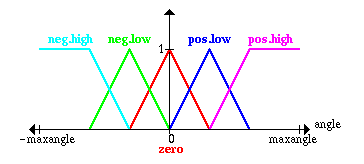
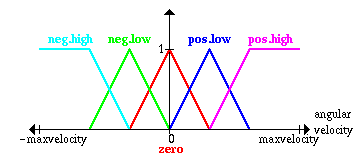
The same is done for the angle between the platform and the pendulum
and the angular velocity of this angle:


Please notice that, to make it easier, we assume that in the beginning the pole is in a nearly upright position so that an angle greater than, say, 45 degrees in any direction can - by definition - never occur.
On the next page we will set up some rules that we wish to apply in certain situations.