We can interpret the elements which have assigned the number 1 as The elements are in the set A and the elements which have assigned the number 0 as The elements are not in the set A.
The very basic notion of fuzzy systems is a Fuzzy (sub)set.
In classical mathematics we are familiar with what we call crisp sets.
Here is an example:
First we consider a set X of all real numbers between 0 and 10 which
we call the universe of discourse. Now, let's define a subset A
of X of all real-numbers in the range between 5 and 8.
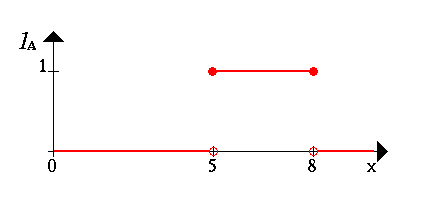
A = [5,8]
We now show the set A by its characteristic function, i.e. this function
assigns a number 1 or 0 to each element in X, depending on whether the element
is in the subset A or not. This results in the following figure:

We can interpret the elements which have assigned the number 1 as
The elements are in the set A and the elements which have assigned
the number 0 as The elements are not in the set A.
This concept is sufficient for many areas of applications. But we can easily find situations where it lacks in flexibility. In order to show this consider the following example on the next page: