Froude’s Momentum Theory for an Actuator Disk

The Double-Multiple Streamtube Model

The derivation for this model is based on Strickland’s (1) single multiple streamtube model extended to the double streamtube model as described by Paraschivoiu (2) . The derivation is essentially the as for Froude’s actuator disk and the blade element calculation is posed in a slightly different manner than Glauerts.

One way to provide parameters for characterising energy conversion by a vertical axis Darreius type MCT is to use Froude's actuator disc theory applied to two sets of multiple streamtubes across the rotor as illustrated below. Based on the following assumptions Glauert’s blade element model is adapted and an algorithm created following Strickland’s approach. The Paraschivoiu approach will be discussed after.

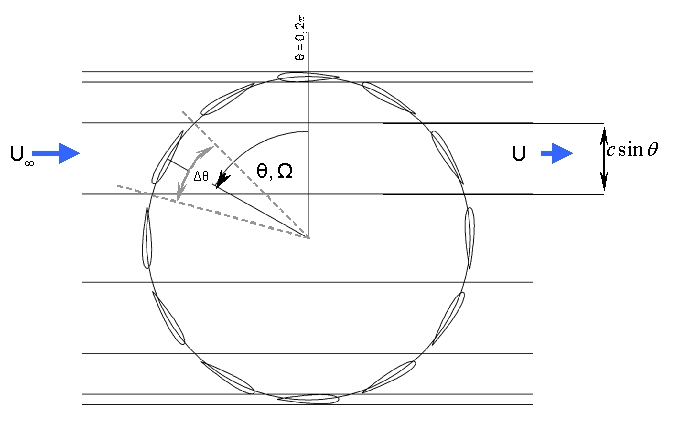
The schematic of the aerodynamic model shown in the figure above indicates a streamtube passing through the rotor, with dimensions shown with depth equal to blade height. The stream tube passes though the rotor and the blades pass through the streamtube, which is essentially stationary, extracting energy and thus reducing the streamtube velocity from the freestream to u₂ as with the standard actuator disk theory.

Time averaging the axial momentum equation (Eqn 12 in Froude) and utilising Bernoulli’s equation as before we have the average streamwise force in terms of freestream and reduced velocities of a blade element passing throught the streamtube:

Eqn 1 with

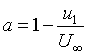Eqn 2 as before

And relating the average force in the streamtube to the streamwise force F_x of a blade element passing through it, noting that each of N blade elemtns spend percent of their time in the streamtube, thus:

 

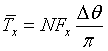Eqn 3

and noting

Eqn 4

we have

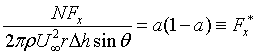Eqn 5

Now consider the following blade element at arbitrary azimuthal position .

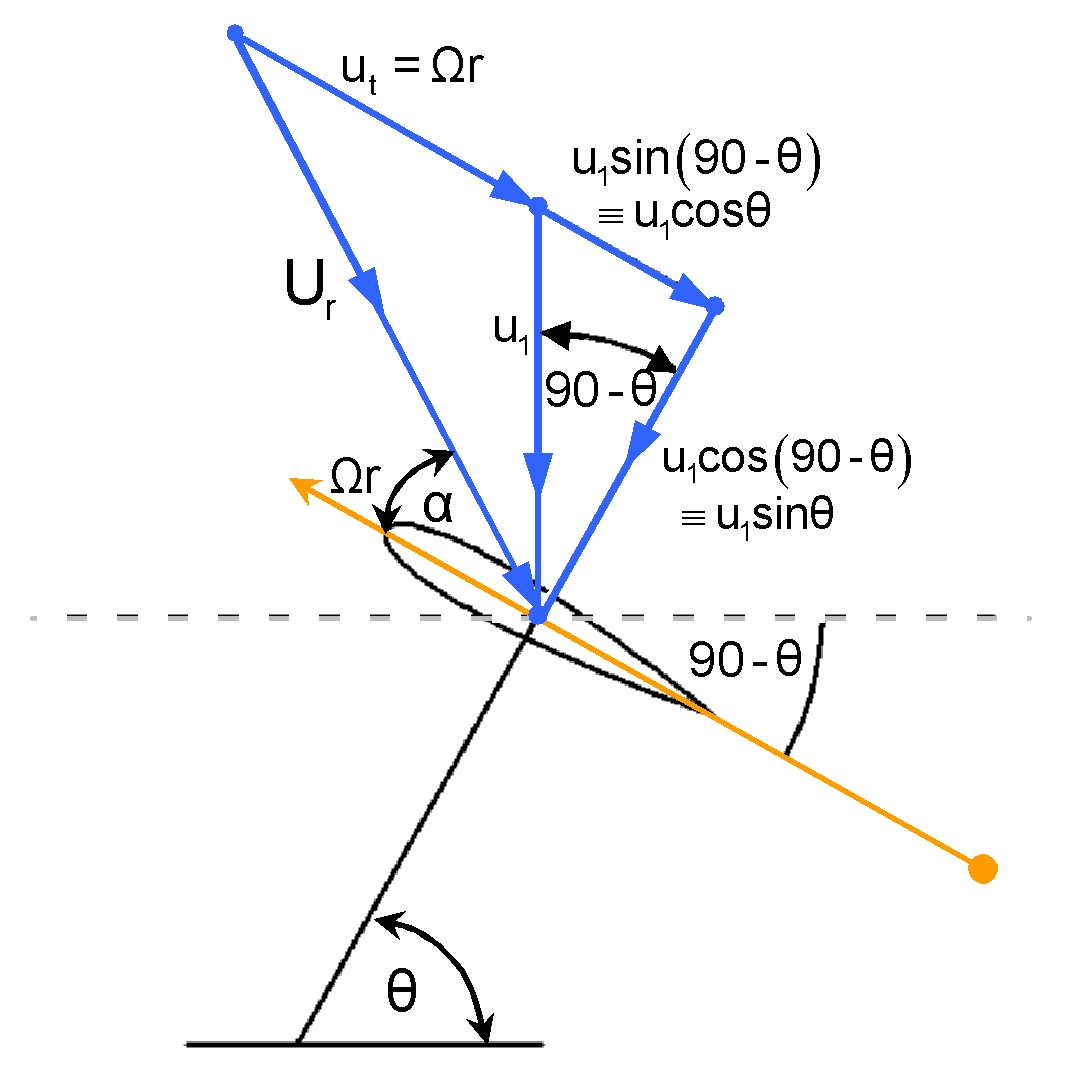
We have the blade hydrodynamic incidence given by:

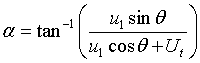
Eqn 6

Eqn 7

and the resultant velocity by Eqn. 7

And it is noted that according to classical aerodynamics the lift of an aerofoil acts perpendicularly to the freestream and drag acts parallel to it, one may relate the non-dimensional streamwise force given by the LHS of Eqn. 5 to the section properties:

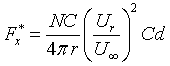Eqn 8

however since it is the tangential force which is the torque producer this may more aptly be expressed

Eqn 9

With C_n & C_t as defined previously. Now considering the RHS of Eqn. 5 may be written

Eqn 10

We now have all the equations required to attempt a solution of the Momentum Equation. A similar iterative procedure is carried out on a as in the “straight” blade element method:

1. axial induction factor a defined equal to zero
2. obtained from Eqn. 6 thus aerofoil coefficients obtained from lookup table
3. Ur from Eqn. 7
4. F_x* computed by Eqn. 9
5. Present values of a and F_x* used in RHS of Eqn. 10 for next value of a
6. u₁ from definition of and iterate until convergence

The momentum equation now solved, the blade element contribution torque contribution as it passes through the streamtube is calculated as

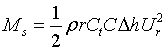Eqn 11

Which is summed over the Ns blade elements to give the blade torque contribution at azimuthal station. The average rotor torque produced by N blades at N_t values of M_s is given by

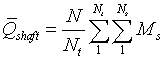Eqn 12

And so .

An interesting dynamic problem not modelled, but which is likely to be encountered in this type of system is that of dynamic stall, described more here.

The double multiple streamtube refinement makes the assumtption that the flow has reached it’s far wake velocity by the time the streamtube is passed through by a blade element for the second time, ie. that the inflow velocity for streamtubes experienced by blades whose azimuthal position is is given by

Eqn 13

This assumption is theoretically tenuous, as it is unlikely that the wake will be fully developed in time, however, correlation with experimental results make this the de rigueur calculation scheme (until very recently).

Initial validation was done against small scale turbine work carried out by Kiho & Shionio et al (5)(6)(7)in several experimental studies, and compares favourably in terms of description of device performance characteristics at varying tip speed ratios.

back to top

References & Bibliography

1	STRICKLAND, J., SAND75-0413: The Darrieus Turbine: A Performance Prediction Model Using Multiple Streamtubes, 1975 Sandia National Laboratories, Albuquerque
2	PARASCHIVOIU, I. Ireq's Aerodynamic Model Based on Two Actuator-Disks Theory for Darrieus Wind Turbines. 1986. Montreal, Que, Can: Pergamon Press, New York, NY, USA.
3	PARASCHIVOIU, I., et al. Some Refinements to Aerodynamic-Performance Prediction for Vertical-Axis Wind Turbines. 1986. San Diego, CA, USA: American Chem. Soc.
4	KLIMAS, P. and SHELDAHL, R., SAND78-0014: Four Aerodynamic Prediction Schemes for Vertical-Axis Wind Turbines: A Compendium, 1978 Sandia National Laboratories, Alburquerque
5	KIHO, S. and SHIONO, M., Electric Power Generations from Tidal Currents by Darrieus Turbine at Kurushima Straits. Transactions of the Institute of Electrical Engineers of Japan, Part D, 1992. 112-D(6): p. 530-8.
6	KIHO, S., et al., Power Generation from Tidal Currents by Darrieus Turbine. Renewable Energy, 1996. 9(1-4): p. 1242-1245.
7	KIHO, S., et al. Study on the Power Generation from Tidal Currents by Darrieus Turbine. 1996. Los Angeles, CA, USA: Int Soc of Offshore and Polar Engineerns (ISOPE), Golden, CO, USA.
8	BRAHIMI, M.T., et al. Darrieus Rotor Aerodynamics Using a Three-Dimensional Wind Simulation. 1989. Glasgow, UK: Peter Peregrinus.
9	BRAHIMI, M.T. and PARASCHIVOIU, I. Darrieus Rotor Aerodynamics in Turbulent Wind. 1991. Boston, MA, USA: ANS.
10	SHIONO, M., et al., Experimental Study of the Characteristics of a Darrieus Turbine for Tidal Power Generation. Electrical Engineering in Japan (English translation of Denki Gakkai Ronbunshi), 2000. 132(3): p. 38-47.
11	KLIMAS, P. and SHELDAHL, R., SAND80-2114: Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines, 1981 Sandia National Laboratories, Albuquerque
12	MOLLAND, A.F., et al., Measurements and Predictions of Forces, Pressures and Cavitation on 2-D Sections Suitable for Marine Current Turbines. Proceedings of the Institution of Mechanical Engineers Part M: Journal of Engineering for the Maritime Environment, 2004. 218(2): p. 127-138.
13	CAMPOREALE, S.M. and MAGI, V., Streamtube Model for Analysis of Vertical Axis Variable Pitch Turbine for Marine Currents Energy Conversion. Energy Conversion and Management, 2000. 41(16): p. 1811-27.
14

 

 

Froude’s Momentum Theory for an Actuator Disk

Go back to Contents