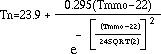
PMV represents the 'predicted mean vote' (on the thermal
sensation scale) of a large population of people exposed to
a certain environment. PMV is derived from the physics of
heat transfer combined with an empirical fit to sensation.
PMV establishes a thermal strain based on steady-state heat
transfer between the body and the environment and assigns a
comfort vote to that amount of strain. PPD is the predicted
percent of dissatisfied people at each PMV. As PMV changes
away from zero in either the positive or negative direction,
PPD increases.
The PMV equation for thermal comfort is a steady-state model. It is an empirical equation for predicting the mean vote on a ordinal category rating scale of thermal comfort of a population of people. The equation uses a steady-state heat balance for the human body and postulates a link between the deviation from the minimum load on heat balance effector mechanisms, eg sweating, vaso-constriction, vaso-dilation, and thermal comfort vote. The greater the load, the more the comfort vote deviates from zero. The partial derivative of the load function is estimated by exposing enough people to enough different conditions to fit a curve. PMV (Predicted Mean Vote), as the integrated partial derivative is now known, is arguably the most widely used thermal comfort index today. The ISO (International Standards O rganization) Standard 7730 (ISO 1984), "Moderate Thermal Environments -- Determination of the PMV and PPD Indices and Specification of the Conditions for Thermal Comfort," uses limits on PMV as an explicit definition of the comfort zone.
The PMV equation only applies to humans exposed for a
long period to constant conditions at a constant metabolic
rate. Conservation of energy leads to the heat balance
equation:
H-Ed-Esw-Ere-L=R+C
Where:
H = internal heat production
Ed = heat loss due to water vapour diffusion through the skin
Esw = heat loss due to sweating
Ere = latent heat loss due to respiration
L = dry respiration heat loss
R = heat loss by radiation from the surface of the clothed body
C = heat loss by convection from the surface of the clothed body
The equation is expanded by substituting each component with a function derivable from basic physics. All of the functions have measurable values with exception of clothing surface temperature and the convective heat transfer coefficient which are functions of each other. To solve the equation, an initial value of clothing temperature is estimated, the convective heat transfer coefficient computed, a new clothing temperature calculated etc., by iteration until both are known to a satisfactory degree.
Now let us assume the body is not in balance and write
the heat equation as:
L = H-Ed-Esw-Ere-L-R-C,
where L is the thermal load on the body.
Define thermal strain or sensation, Y, as some unknown function of L and metabolic rate. Holding all variables constant except air temperature and metabolic rate, we use mean votes from climate chamber experiments to write Y as function of air temperature for several activity levels. Then substituting L for air temperature, determined from the heat balance equation above, evaluate the partial derivative of Y with respect to L at Y=0 and plot the points versus metabolic rate. An exponential curve is fit to the points and integrated with respect to L. L is simply renamed "PMV" and we have (in simplified form):
PMV = exp[met]*L.
Where:
L=F(Pa,Ta,Tmrt,Tcl)
PMV is "scaled" to predict thermal sensation votes on a seven point scale (hot, warm, slightly warm, neutral, slightly cool, cool, cold) by virtue of the fact that for each physical condition, Y is the mean vote of all subjects exposed to that condition. The major limitation of the PMV model is the explicit constraint of skin temperature and evaporative heat loss to va lues for comfort and "neutral" sensation at a given activity level.
ET*- DISC also uses a heat balance model to predict thermal comfort, but the model evolves with time rather than being steady-state like PMV. ET* stands for New Effective Temperature where "effective temperature" is an temperature index that accounts for radiative and latent heat transfers. ET* can be calculated using the '2-Node' model. The 2-node model determines the heat flow between the environment, skin and core body areas on a minute by minute basis. Starting from an initial condition at time=0, the model iterates until equilibrium has been reached (60 minutes is a typical time). The final mean skin temperature and skin wettedness are then associated with an effective temperature. DISC predicts thermal discomfort using skin temperature and skin wettedness.
The 2-node model was introduced in 1970 specifically to formulate a new effective temperature scale. The purpose was to determine particular combinations of physical conditions producing equal physiological strain. Backed by extensive data from climate chamber experiments, it was determined that while skin temperature is a good indicator of thermal comfort sensation in cold environments, skin wettedness is a better indicator in warm environments where sweating occurs because skin temperature changes are small by comparison. The model represents the human body as two concentric cylinders, a core cylinder and a thin skin cylinder surrounding it. Clothing and sweat are assumed to be evenly distributed over the skin surface. At time "zero", the cylinder is exposed to a uniform environment, and the model produces a minute-by-minute simulation of the human thermoregulatory system. After the user-specified time period is reached, the final surface temperature and surface skin wettedness of the cylinder are used to calculate ET*, SET*, and other indices. ET* is the temperature of an environment at 50% relative humidity in which a person experiences the same amount heat loss as in the actual environment.
SET*SET* numerically represents the
thermal strain experienced by the cylinder relative to a
"standard" person in a "standard" environment. SET* has the
advantage of allowing thermal comparisons between
environments at any combination of the physical input
variables, but the disadvantage of also requiring "standard"
people.
Based on a laboratory study with a large number of subjects, empirical functions between two comfort indices, and skin temperature and skin wettedness, were developed. These functions (both linear) are used in the 2-Node model to produce predicted values of the votes of populations exposed to the same conditions as the cylinder.
TSENS, DISCTSENS, the
first index, represents the model's prediction of a vote on
the seven point thermal sensation scale. DISC, the second
index, predicts a vote on a scale of thermal
discomfort:
DISC:
Intolerable
Very uncomfortable
Uncomfortable
Slightly uncomfortable
Comfortable
The 2-Node model has undergone many iterations and
refinements. In the most recent iteration, a new
temperature index, PMV*, that incorporates skin wettedness
into the PMV equation using SET* or ET* to characterize the
environment.
Apart from the thermal comfort models described above, there are many more theoretical models, both deterministic and empirical. Some empirical models with application to building design and/or environmental engineering are outlined below.
PD or "predicted
percent dissatisfied due to draft", is a fit to data of
persons expressing thermal discomfort due to drafts. The
inputs to PD are air temperature, air velocity , and
turbulence intensity. PS is a fit to data of comfortable
persons choosing air velocity levels. The inputs to PS are
operative temperature and air velocity. TS is a fit to data
of thermal sensation as a linear function of air temperature
and partial vapour pressure.
A 'draft' is unwanted local cooling. The draft risk (or
PD) equation is:
PD=3.413(34-Ta)(v-0.05)0.622+0.369vTu(34-Ta)(v-0.05)0.622
Tu is the turbulence intensity expressed as a percent. 0
represents laminar flow and 100% means that the standard
deviation of the air velocity over a certain period is of
the same order of magnitude as the mean air velocity. v is
the air velocity (in meters per second) and Ta is the air
temperature in degrees Celsius. The PD equation arises from
two studies in which 100 people were exposed to various
combinations of air temperature, air velocity, and
turbulence intensity. For each combination of conditions,
the people were asked if they felt a draft. PD represents
the percent of subjects who voted that they felt a draft for
the selected conditions.
The PS equation predicts the air velocity that will be
chosen by a person exposed to a certain air temperature when
the person has control of the air velocity source. The PS
equation is
PS=1.13SQRT(Top)-0.24Top+2.7SQRT(v)-0.99v
Top is operative temperature (in degrees Celsius) and v
is the air velocity in meters per second. The PS equation
arises from a study in which 50 people were asked to adjust
an air velocity source as they pleased when exposed to a
specific air temperature. PS represents the cumulative
percent of people choosing a particular air velocity at the
specific temperatures tested in this experiment
TS is an equation that predicts thermal sensation vote
using a linear function of air temperature and partial vapour
pressure. The TS equation is:
TS=0.245Ta+0.248p-6.475
Ta is the air temperature in degrees Celsius and p is the
partial vapour pressure in kilo-pascals. The TS equation
arises from a study similar to the PMV-PPD study described
above.
Adaptive models include in some way the variations in
outdoor climate for determining thermal preferences indoors.
An adaptive model developed by Auliciems fits sensation
data based on field investigations of thermal comfort in
Australia spanning several climates. Auliciems equation
is:
Tn=9.22+0.48Ta+0.14Tmmo
Humphreys equation is a fit to considerable data for
climate-controlled and non-climate controlled buildings:
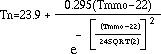
For both the Auliciems and Humphreys models, Tn is the
neutral temperature, Ta is the air temperature, and Tmmo is
the mean monthly outdoor temperature.