
The CIBSE method of determining the peak inside environmental temperature requires the following to be calculated in turn:
An Example
Consider an office of internal dimensions 4m x 5m x 3m high with one external wall of dimension 4m x 3m high incorporating a window of dimension 3.5m x 2m high. Other relevant data include:
| Windows: | single glazed, no shading, facing south |
| Floor: | linoleum on concrete, no carpet. |
| Ceiling: | plastered concrete. |
| Partitions: | plastered brickwork. |
| Occupancy: | 4 persons for 8 hours (80W each). |
| Lighting: | 30 W/m2 of floor area, on 0700-0900 and 1700-1900. |
| Classification: | heavyweight |
The objective is to estimate the peak internal environmental temperature likely to occur during a sunny period in August.
Mean Solar Heat Gain

The solar gain factor, S, represents the proportion of radiation which eventually enters the space: some being absorbed in the glass, some reflected and some re-transmitted to the outside. In this case therefore:

Mean Casual Gains
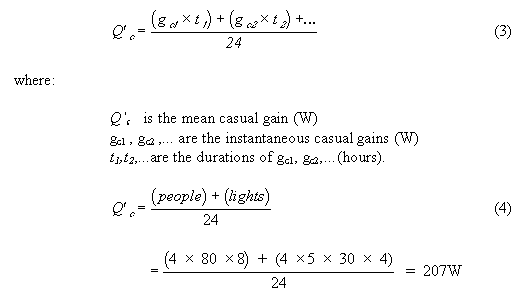
Total Mean Heat Gain

Mean Internal Environmental Temperature

where g and f refer to glazed and opaque surfaces respectively and Cv is the ventilation conductance evaluated from:

From Table A9/4 Nv = 0.3 W/m3K and so in this case:

From Table A8.3 the mean outside air temperature, T'ao is 17°C and from Table A6.20 the mean solair temperature, T'eo, is 25.6°C. Therefore from equation (6):

Swing (mean-to-peak) in Heat Gain
The variation in heat input due to solar radiation, outside temperatures and casual gains are now determined and added to give the total swing in heat input.
In order to determine the swing it is necessary to decide on the time of day when the peak indoor temperature is likely to occur, and compute the mean-to-peak effective heat inputs from this peak hour. If there is doubt about the peak hour, the same procedure must be followed for several hours to ensure that the peak hour is located.
Swing in Effective Solar Heat Gain
From Tables A8.1 and A6.24 - A6.36, the difference between the solar radiation intensity at the peak hour and the mean intensity may be found in order to give the effective heat input.
Alternating Solar Gain Factor
The solar radiation intensity incident on the glazing is modified to give the effective heat input to the air in the room as a result of the following factors:
Thus, to take account of the lag associated with surface factors, in heavyweight rooms a time lag of 1 hour is assumed, i.e. the radiation incident on the surface at 1 hour earlier should be used. For lightweight structures, no allowance is made.

Suppose that it is required to determine the peak internal environmental temperature at 1200h; allowing 1 hour lag, we take the intensity Ip at 1100h = 565 W/m^2, therefore:

Structural Gain

Assuming a wall comprising: 220mm brickwork, 28mm air-gap and 10mm
plasterboard, where f = 0.4 and
 = 7h; also Teo at 0500h (1200 - 7) = 11.8°C and
T'eo = 25.6°C. Therefore:
= 7h; also Teo at 0500h (1200 - 7) = 11.8°C and
T'eo = 25.6°C. Therefore:

It is usual for this value to be small in the UK and so it is often neglected.
Casual Gain

Swing in Gain, Air-to-Air
The difference between the outdoor air temperature at the peak hour and the mean outdoor air temperature must now be found in order to obtain the variation in heat input due to the outside temperature swing. This temperature difference (see Table A8.3) is then multiplied by the area and U-value of exposed glass, and by the appropriate ventilation heat loss.

Total Swing

Swing in Internal Environmental Temperature
In order to maintain the temperature of the room at the same value as the mean external temperature, 1472W would need to be extracted. It is now assumed that the outside air temperature remains constant and that a source in the room produces 1472W. This heat will be lost by ventilation and by the thermal admittance of the room's surfaces:

From Table A8.7 (or by calculation), the Y values are obtained as follows:

Peak Internal Environmental Temperature

Generalised Solutions
See pages A8.8 and A8.9 (Figure A8.4) for different cases.